今回はおそらく午前問題で落第な気がしますが、今後に活かすために問題の解き方を書いて聞こうと思います。今回は、基本情報技術者試験からの出題が多かったそうです。自分は応用情報から受けていたので、この範囲はカバーしていませんでした。具体的に自分が解けなかった問題として、線形計画法が挙げられます。計算問題は結構凡ミスが多く落としたものが多かったと思いますが、この問題に関しては全く解けなかったです。しかも線形計画法の問題だけ何故か2問出題されたので印象深いです。
線形計画法の解き方
問75 製品X, Yを1台製造するのに必要な部品数は、表のとおりである。製品1台当たりの利益がX, Yともに1万円のとき, 利益は最大何万円になるか。ここで, 部品Aは120個, 部品Bは60個まで使えるものとする。
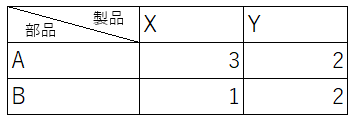
ア 30 イ 40 ウ 45 エ 60
この問題は部品数に対して制約をかけ、利益(ともに1万円なので今回は個数の総和)を最大化することを目標とします。
制約は以下の通りです。
- 0≦X, 0≦Y…個数なので負の数にならないことを示す制約。
- 3X+2Y≦120, X+2Y≦60…問題文中の制約。部品Aによる制約で、どれだけXとYを作ろうとしても事前に準備できる部品Aの個数は超えられないことを示す。
- X+2Y≦B…制約2の部品B version
ここで利益=10000(X+Y)を最大化するようにA, Bを選択する必要があるが、今回はそれぞれの利益がともに10000円であるため、X+Yの個数を最大化することと同じである。A, Bに対して制約2, 3の式を代入し、それを線形な式と考え横軸x, 縦軸yのグラフとして記述します。今回の場合、3X+2Y=120とX+2Y=60です。x軸, y軸(制約1)およびこれらの式で囲まれる面積が、今回取りうる値の範囲です。
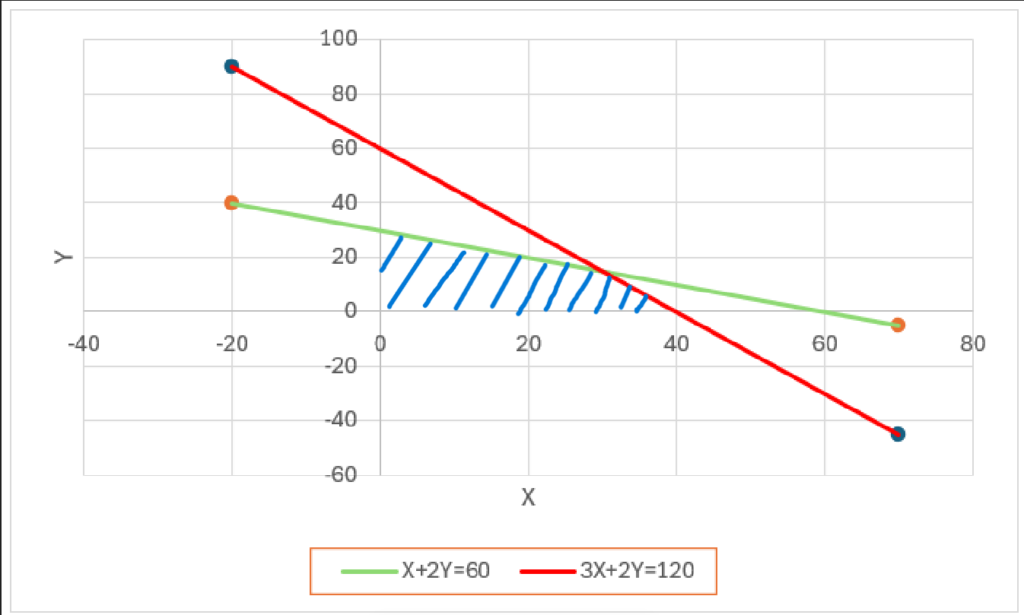
図1 線形計画法のグラフ
この図のx軸, y軸, X+2Y=60, 3X+2Y=120で囲まれた範囲(=青の斜線の部分)の内1点選択し、その時の座標の合計値が最大のものをとってきます。図1では、検討すべき座標は四角形の角である(0,0), (40,0), (0,30), (30,15)の4点です。ここで座標の合計値が最も大きいのは(30,15)であるため、答えは45→ウであると考えられます。
四角形の角以外は無視してよい理由
角以外の頂点を考慮する必要がない理由ですが、このグラフが凸集合である性質を利用すると理解できます。任意の頂点の座標をB(b1,b2), C(c1,c2)とし、その間の点(=頂点でない座標)をA(a1,a2)とすると、凸結合という性質と0<K<1となるKを用いて、以下の関係で記述できます。
a1=Kb1+(1-K)c1
a2=Kb2+(1-K)c2
これは線分の内分の公式と同じですが、図1の青い斜線の部分が内側に凹んでおらず、2点間の任意の点が青い斜線の部分に含まれる必要があります(=凸性)。凹んでいたら凸ではないですからね(哲学)。a1, a2はそれぞれ
min(b1,c1)<a1<max(b1,c1),
min(b2,c2)<a2<max(b2,c2)
と表せます。 このような点でのX, Yの倍率が等しい最大化関数Z=X+Yでは、Zの値も中間点となります。K=1/2のときは2点間の平均値と同じなのでイメージしやすいと思います。よって角の座標のzの片側は常に線分上のそれ以外の座標のz値よりも大きくなるのです(もう片側は必ず中間点よりも小さい)。
今話したのは頂点間の線分上の任意の中間点でしたが、小さいことが示された任意の中間点と頂点を結ぶ線分上の点での凸結合でも同様です。これにより面積内の全ての点で証明済みの中間点と任意の頂点との中間点のz値が小さくなるため、この比較作業を十分に行うと、角の点が最大/最小を持つことになります。これが角の点のみを検討すればよい理由となります。
