前回に引き続きなぜか2問出題された線形計画法の2問目を解いていきます。
問77 表のような製品A, Bを製造, 販売する場合, 考えられる利益は最大で何円になるか。 ここで, 機械の年間使用可能時間は延べ15,000時間とし, 年間の固定費は製品A,Bに関係なく15,000,000円とする。
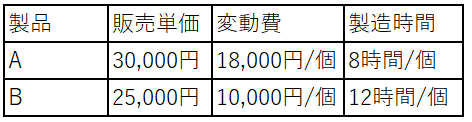
ア 3,750,000 イ 7,500,000 ウ 16,250,000 エ 18,750,000
ここで、x=Aの個数, y=Bの個数とすると制約は
8x+12y≦15000, x≧0, y≧0
この条件下で、利益=販売単価-変動費-固定費
30,000x+25,000y-18,000x-10,000y-15,000,000
=12,000x+15000y-15,000,000
を最大化することを目的とします。前回の問題と異なるのは、個数にかかる制約を除き、制約が一つしかないことです。これは問題が非常に簡単に解けることを意味します。連立方程式を解いてその間の面積についての議論を省略できるためです。
それぞれの時間当たりの利益は以下になります。
A:1500円/時 (30,000 円-18,000 円)/8 時間/個
B:1250/時 (25,000円-10,000円)/12 時間/個
Aの時間当たりの利益が大きいことから、Aを制約(年間15,000時間)限界まで生産→残りの時間リソースをBに費やすという方向性で解決できそうです。Aの限界生産数は年間使用可能時間/Aの製造時間
15,000/8=1875 個
ここで少数になる(=余りが出る)ならBの生産を考慮すべきですが、今回はAをフルパワー生産するだけで最大利益を得られることを示しています。今計算したのは個数なので、最大利益は一時間当たりの利益×年間使用可能時間-固定費で
1500×15,000-15,000,000=7,500,000 円
あるいは最大生産数×一個当たりの利益-固定費で
1875×(30,000-18,000)-15,000,000=7,500,000 円
ということでイが正解となります。
自分の問題用紙に書いておいた答えを見ると、イを選択していました。この問題は正解のようですがおそらく悲しい結果になっていると思います。。。(泣)
